이진 탐색

Binary Search

정렬되어 있는 데이터에서 특정한 값의 위치을 찾는 알고리즘이며, 시간 복잡도는 O(log₂N) 이다.

stl 에 세 가지 이진 탐색 함수가 존재하고 목적에 따라 구현 방식이 조금씩 다르다.

binarySearch()

정렬된 리스트에서 고유한 값을 찾을 때 사용.

C++

int binarySearch(int k, int n, vector<int> a) {
    int m;
    int l = 0;
    int r = n - 1;
    
    while(l <= r) {
        m = (l + r) / 2;
        
        if(a[m] < k) {
            l = m + 1;
        } else if(a[m] > k) {
            r = m - 1;
        } else {
        	return m;
        }
    }
    
    return -1;
}

lowerBound()

중복이 존재할 수 있고, 찾으려는 값과 정확히 일치하는 값이 없을 수 있다.

정렬된 리스트에서 크거나 같은 데이터 중, 가장 작은 값을 찾을 때 사용.

C++

int lowerBound(int k, int n, vector<int> a) {
    int m;
    int l = 0;
    int r = n;
    
    while(l < r) {
        m = (l + r) / 2;
        
        if(a[m] < k) {
            l = m + 1;
        } else { /* 값이 같으면 왼쪽으로 이동한다. */
            r = m;
        }
    }
    
    return r;
}

key 이상의 값이 나타나는 최소 위치이므로 현재 값이 key보다 크거나 같을 때 right 를 middle - 1 값이 아닌 middle 값으로 설정해준다.

배열 a에 존재하는 모든 값이 key값 보다 작을 경우는 n를 반환한다. (a의 범위는 [0, n-1]. 배열의 범위를 벗어나는 값.)

upperBound()

중복이 존재할 수 있고, 찾으려는 값과 정확히 일치하는 값이 없을 수 있다.

정렬된 리스트에서 주어진 값보다 크면서, 가장 작은 값을 찾을 때 사용.

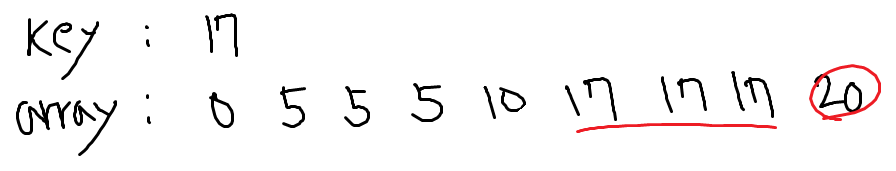
C++

int upperBound(int k, int n, vector<int> a) {
    int m;
    int l = 0;
    int r = n;
    
    while(l < r) {
        m = (l + r) / 2;
        
        if(a[m] <= k) { /* 값이 같으면 오른쪽으로 이동한다. */
            l = m + 1;
        } else {
            r = m;
        }
    }
    
    return r;
}

key 를 초과하는 값이 나타나는 최소 위치이므로 현재 값이 key보다 클 때 right 를 middle - 1 값이 아닌 middle 값으로 설정해준다.

배열 a에 존재하는 모든 값이 key값 보다 작거나 같을 경우는 n를 반환한다. (a의 범위는 [0, n-1]. 배열의 범위를 벗어나는 값.)

참고

• https://cplusplus.com/reference/algorithm/lower_bound/
• https://cplusplus.com/reference/algorithm/upper_bound/