힙 (heap)
힙은 완전 이진 트리 기반의 자료구조로 여러 개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아낼 수 있다.
종류에는 최대 힙(max heap), 최소(min heap) 두 가지가 있다.
힙의 구현
힙은 완전 이진 트리이기 때문에 각각의 노드에 번호를 붙일 수 있다. 이 번호를 배열의 인덱스로 생각하면 배열에 히프의 노드들을 저장할 수 있다.
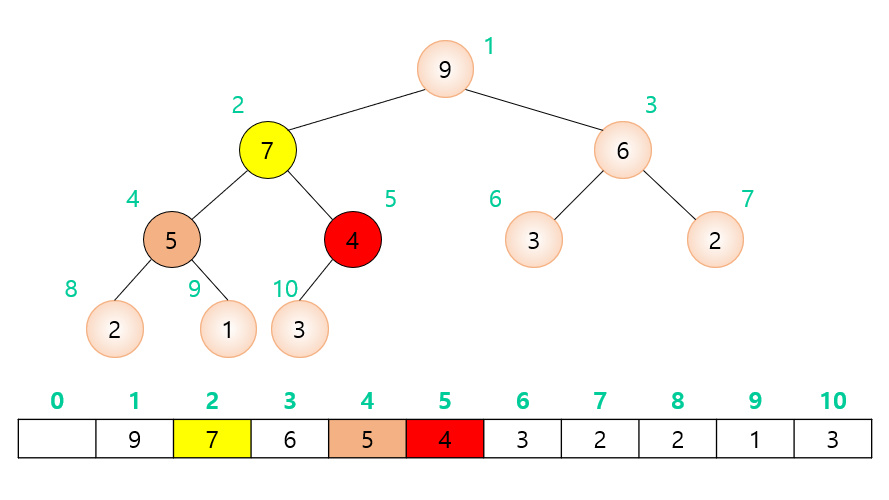
어떤 노드의 자식과 부모를 인덱스로부터 찾기 위하여 루트노드의 시작 번호는 1번으로, 배열의 0번째 인덱스는 사용하지 않는다.
- 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
- 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
- 부모의 인덱스 = (자식의 인덱스) / 2
소스코드
class maxHeap():
def __init__(self, max_size):
self.heap = [None] * max_size
self.heap_size = 0
def insert(self, item):
self.heap_size += 1
i = self.heap_size
while i != 1 and self.heap[i//2] < item:
self.heap[i] = self.heap[i//2]
i = i//2
self.heap[i] = item
def delete(self):
item = self.heap[1] # root node
temp = self.heap[self.heap_size] # last node
self.heap_size -= 1
parent = 1
child = 2
while child <= self.heap_size:
# 현재 노드(1번)의 자식 중 더 큰 자식노드를 찾는다.
if child < self.heap_size and self.heap[child] < heap[child+1]:
child += 1
if temp >= self.heap[child]:
break
# 한단계 아래로 이동
self.heap[parent] = self.heap[child]
parent = child
child *= 2
self.heap[parent] = temp
return item
class minHeap():
def __init__(self, max_size):
self.heap = [None] * max_size
self.heap_size = 0
def insert(self, item):
self.heap_size += 1
i = self.heap_size
while i != 1 and self.heap[i//2] > item:
self.heap[i] = self.heap[i//2]
i = i//2
self.heap[i] = item
def delete(self):
item = self.heap[1] # root node
temp = self.heap[self.heap_size] # last node
self.heap_size -= 1
parent = 1
child = 2
while child <= self.heap_size:
# 현재 노드(1번)의 자식 중 더 큰 자식노드를 찾는다.
if child < self.heap_size and self.heap[child] > heap[child+1]:
child += 1
if temp <= self.heap[child]:
break
# 한단계 아래로 이동
self.heap[parent] = self.heap[child]
parent = child
child *= 2
self.heap[parent] = temp
return item
if __name__ == "__main__":
# max heap
maxH = maxHeap(200)
maxH.insert(10)
maxH.insert(5)
maxH.insert(30)
print("<", maxH.delete(), ">", end=' ')
print("<", maxH.delete(), ">", end=' ')
print("<", maxH.delete(), ">")
# min heap
minH = minHeap(200)
minH.insert(10)
minH.insert(5)
minH.insert(30)
print("<", minH.delete(), ">", end=' ')
print("<", minH.delete(), ">", end=' ')
print("<", minH.delete(), ">")출력
< 30 > < 10 > < 5 >
< 5 > < 10 > < 30 >삽입은 배열의 맨 끝에 요소를 추가하고 최대 힙의 경우 부모노드와 비교하여 삽입노드가 크면 교환한다. 최소 힙의 경우에는 작으면 교환한다.
힙의 응용
'Data Structure' 카테고리의 다른 글
| 그래프 (0) | 2020.08.05 |
|---|---|
| 우선순위 큐 (0) | 2020.08.04 |
| 트리 (0) | 2020.07.31 |
| 덱 (0) | 2020.07.29 |
| 연결 리스트로 구현한 큐 (0) | 2020.07.19 |
댓글