피보나치 함수

피보나치 수열 (Fibonacci Numbers)

첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다.

가장 큰 문제를 방문 후 작은 문제를 호출하여 푸는 Top-down 방식은 순환을 사용하여 구현하고, 작은 문제들부터 값을 구해가며 전체 문제의 답을 찾는 Bottom-up 방식은 반복을 사용하여 구현한다.

순환

1. 비효율적인 순환 알고리즘

피보나치 순환 알고리즘은 이진 트리(Binary tree) 형태를 띄게 된다.

함수를 순환호출 하는 과정은 root -> left -> right 으로 전위 순회에 해당되고 마지막 노드에서 값을 return 하며 계산하는 과정은 left -> right -> root 으로 후위 순회에 해당된다.

정의

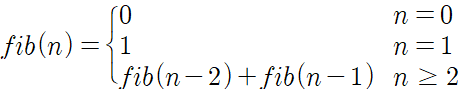
피보나치 수열에 대한 설명을 그대로 정의하면 순환적인 모습을 하고 있다.

소스코드

def fib(n):
    if n <= 1:
        return n
    else:
        return fib(n-2) + fib(n-1)

시간복잡도

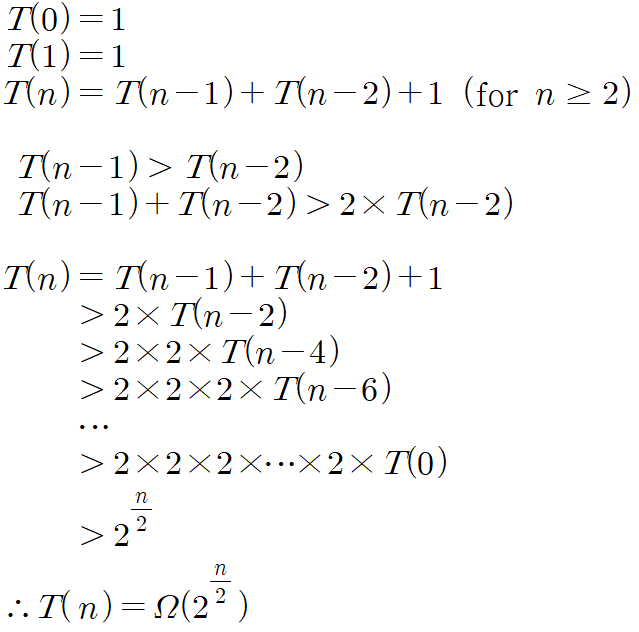
위 소스코드를 시간에 대한 점화식으로 나타낸 후 반복대치를 통해 식을 전개해보자.

조건

비교연산이 한번 이루어지는 T(0) 과 T(1) 시간값은 1이다.

T(n-1) 는 T(n-2) 보다 크므로, T(n-1) 과 T(n-2) 를 더한 값은 T(n-2) 를 두번 곱한 값보다 큼이 명백하다.

계산

주어진 조건에 따라 T(n-1) + T(n-2) 값을 2·T(n) 으로 모두 치환하면 총 n/2 번 2개의 문제들로 나뉘게 된다.

마지막으로 T(0) 값을 1로 치환한 후 빅오 표기법으로 나타내면 복잡도는 O(2^n/2) 가 나온다.

---

+ 순환적인 피보나치 수열을 1부터 n까지 모두 호출하였을 때의 시간복잡도

소스코드

def fib_all(n):
    for i in range(1, n+1):
        print(fib(i))

def fib(n):
    if n <= 1:
        return n
    else:
        return fib(n-2) + fib(n-1)

시간복잡도

복잡도가 O(2^n/2) 인 순환 fib(n) 함수를 n 번 호출한다고 해서 O(n·2^n/2) 복잡도를 가지는 것이 아니다.

자세히 살펴보면 fib_all(n) 는 fib(n) 에 1부터 n까지의 값을 전부 대입해 모든 피보나치 값을 순서대로 출력하는 함수이다.

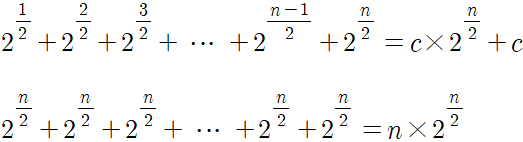
따라서 T(n) = c·2^n/2 + c 이고 빅오 표기법에 따라 상수 c 를 제거했을 때 기존과 동일한 O(2^n/2) 복잡도를 가지게 된다.

---

2. 효율적으로 변경한 순환 알고리즘

메모이제이션(memoization)을 사용하여 함수의 호출을 줄였다.

소스코드

# memoization을 위한 dictionary 선언
dic = {}

def fib_memo(n):

    # 기록되어 있는 값을 바로 return
    if n in dic:
        return dic[n]

    if n <= 1:
        dic[n] = n
        return n
    else:
        dic[n] = fib_memo(n-2) + fib_memo(n-1)
        return dic[n]

시간복잡도

순환 호출이 일어나 트리의 높이(주어진 n)만큼 반복될 때 함수의 중복 호출을 모두 없앰으로써 복잡도는 O(n) 이 된다.

반복

피보나치 수열은 반복 구조를 이용하였을 때 제일 좋은 결과를 얻을 수 있다.

문제가 본질적으로 순환적이게 정의되었다고 해서 꼭 순환적인 방법이 적합한 것은 아니라는 걸 보여준다.

소스코드

def fib_iter(n):
    if n < 2:
        return 0
    else:
        current = 1
        last = 0
        for i in range(2, n+1):
            tmp = current
            current += last
            last = tmp
        return current

시간복잡도

반복문 제어 연산 수를 제외하고 모든 연산을 계산하였을 때 시간 복잡도는 T(n) = 4n - 1 가 나온다. 따라서 복잡도는 O(n).